This is the third post in my automata series, thankfully much shorter than the last one 😆 Here's parts one and two. You can find the companion code for this post here.
Audience Assumptions: Has read parts one and two of this series, or has knowledge of follow set like constructions. Some Python reading skills.
What's a Couple of States, Between Automata?
In the first post I mentioned that reading Andrew Gallant's article on automata instigated me to investigate automata constructions. This is true, but it's not the whole story. I wasn't motivated to build these constructions for myself until I saw a comparison of state diagrams for different automata in the paper 'A Unified Construction of the Glushkov, Follow, and Antimirov Automata' by Cyril Allauzen and Mehryar Mohri [1].
In that paper, figure 1. presents the state diagrams of various automata constructions for the regex (a|b)(a*|ba*|b*)*. I've recreated the state diagrams for Position (Glushkov's) and Follow below.
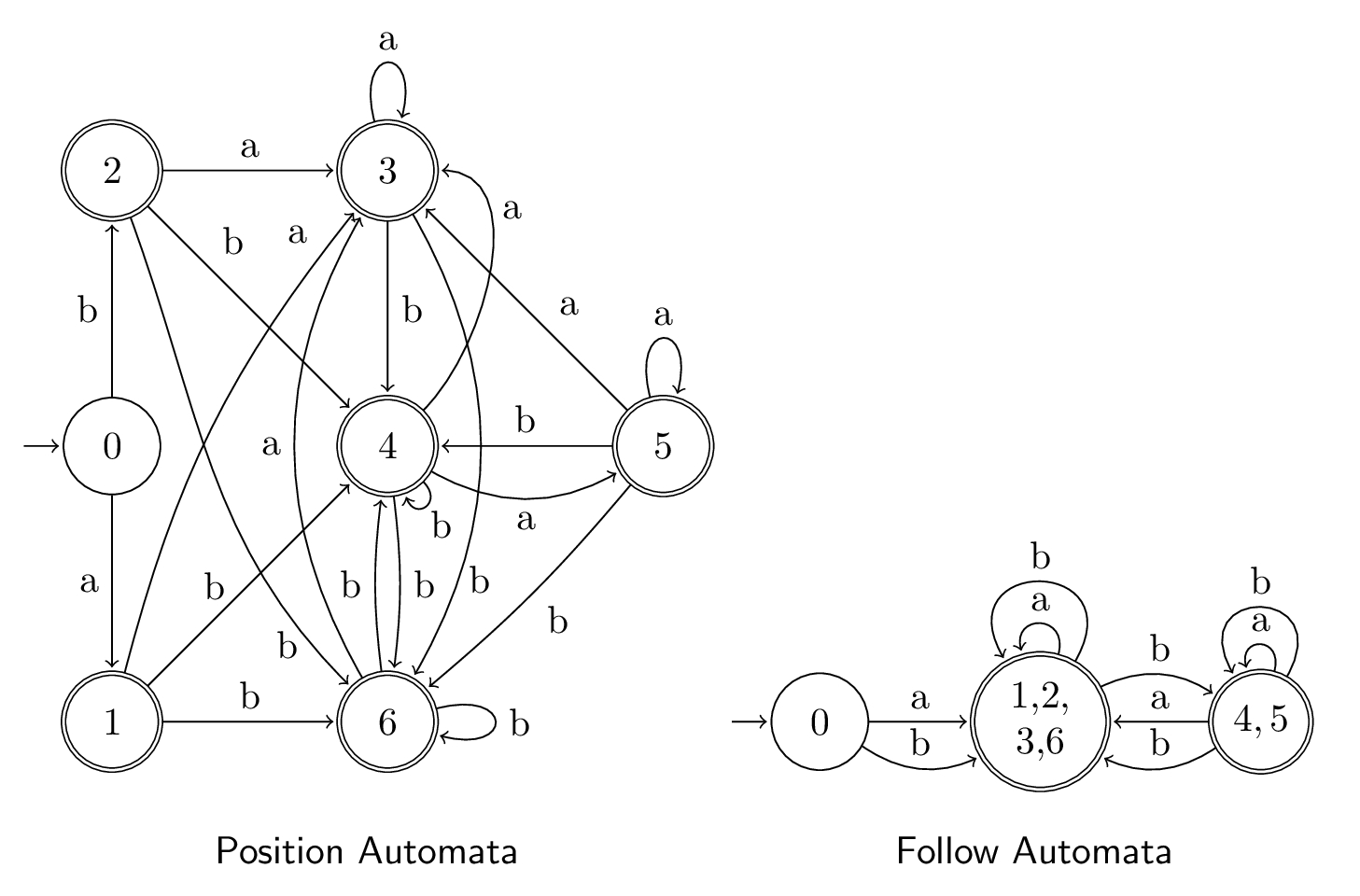
The Follow automata immediately struck me as "better", and there's good reason for this. The time complexity of matching a string with a Non-Deterministic Finite Automata (NFA) depends not just on the length of the string, but also the number of states in the NFA!
This is easy to see when we look at the implementation of accepts (adapted for this example) from our Automata base class:
# overall loop size: word length * num states
def accepts(self, word: str) -> bool:
states = self.initial
# loop size: word length
for symbol in word:
if len(states) == 0:
return False
new_states = set()
# loop size: potentially total number of states in the Automata
# though in practice it's usually less
for s in states:
new_states |= self.transition(s, symbol)
states = new_states
return len(states.intersection(self.final)) > 0
Of course, it's not necessarily true that it would always be faster to run Follow instead of Position, Follow may require significantly more processing to construct for example. None the less, my interest was piqued, and I wanted to build both, which brings us to why I became motivated to write this series of posts: having to implement from academic papers.
I've already broached this topic in both previous posts, so I'll not labour it here, except to again voice my opinion that if the working languages of coders and theorists were closer, then ideas from both sides would see a lot more cross-pollination. I really rate the paper 'On the mother of all automata: the position automaton' [2] by Sabine Broda, Markus Holzer, Eva Maia, Nelma Moreira, and Rogério Reis. It's no coincidence that my writing on this subject has followed its contents so closely.
Okay enough of that, let's get going on understanding Follow automata!
Follow Automata
Quickly before we start, the follow automata was introduce by Lucian Ilie and Sheng Yu [3] all the way back in 2003, but we'll be using the construction provided by Broda et al. instead.
If you've read part one you know the deal by now. Start with the definition and drill down until we reach subjects we know. Let's recap the definition of an automata,
$$A = \langle Q, \Sigma, \delta, I, F \rangle$$
- \(Q\) the set of states.
- \(\Sigma\) the set of symbols (or alphabet).
- \(\delta\) the transition function.
- \(I\) is the initial state.
- \(F\) is the set of final states.
We will be using definitions from part one also, not surprising since \(\mathcal{A}_{\text{F}}\) is an extension of \(\mathcal{A}_{\text{POS}}\). I'll reintroduce these as they are used, and note that I'll be using the non-constructive definitions from Broda et al. verbatim. Upfront, recall that,
- \(\Sigma\) is the set of symbols, \(\sigma\in\Sigma\) is a single symbol, and \(\sigma_{i}\) is a marked symbol.
- \(\alpha\) is a regex, like
ab|a*. - \(\overline{\alpha}\) is a marked regex, like \(a_{1}b_{2}|a_{3}*\).
- \(\textsf{Pos}(\alpha) =\) all marked symbol indexes in \(\overline{\alpha}\).
Now the definition of the Follow automata,
$$\mathcal{A}_{\text{F}}(\alpha) = \langle \textsf{F}(\alpha), \Sigma, \delta_{\text{F}}, (\textsf{Follow}(\alpha, 0), \varepsilon(0)), F_{\text{F}} \rangle$$
An immediate difference: states in \(\mathcal{A}_{\text{F}}\) are not integers! They are instead pairs (or 2-tuples), and this is where we'll start digging.
Initial State \((\textsf{Follow}(\alpha, 0), \varepsilon(0))\)
The first part of the pair we've already seen.
$$ \begin{align} &\textsf{Follow}(\alpha, 0) = \textsf{First}(\alpha) \\[5pt] &\textsf{First}(\alpha) = \{i \mid \sigma_{i}w\in \mathcal{L}(\overline{\alpha})\} \end{align} $$
We haven't encountered \(\varepsilon(0)\) before, though it's similar in form to nullable in Broda et al. Whereas \(\varepsilon(\alpha)\) (nullable) applies to regexes, \(\varepsilon(q)\) (finality) acts on states. Intuitively, it indicates whether a state is final or not.
I want us all to be careful here. When defining \(\mathcal{A}_{\text{F}}\) we will see \(\varepsilon(0)\), \(\varepsilon(1)\), and so on. Now, \(0\) and \(1\) are not states of \(\mathcal{A}_{\text{F}}\), but of \(\mathcal{A}_{\text{POS}}\). So we need to be careful about the two sets of states at play in these definitions. To be clear, these two sets are \(\textsf{Pos}_{0}(\alpha)\) from \(\mathcal{A}_{\text{POS}}\), and \(\textsf{F}(\alpha)\) from \(\mathcal{A}_{\text{F}}\).
For \(q\in Q\) (the set of states), and \(F\) (set of final states), the finality function is defined as,
$$ \varepsilon(q) = \begin{cases} \varepsilon \text{ if }q \in F\\ \emptyset \text{ otherwise} \end{cases} $$
This is simple enough, let's quickly look at an example anyway. Let \(\alpha = (a{*}|b)a\), so \(\overline{\alpha} = (a_{1}{*}|b_{2})a_{3}\). \(F\) will be \(\textsf{Last}_{0}(\alpha)\), \(\textsf{Last}_{0}(\alpha) = \{3\}\), hence \(\varepsilon(0) = \emptyset\).
The key insight of the Follow construction is to label states with their follow sets, rather than position indexes (as in \(\mathcal{A}_{\text{POS}}\)). The total number of states may be reduced as the follow sets of two states may be identical. But we still need to distinguish final from non-final ones, which is done with the second member of the pair.
Set of States \(\textsf{F}(\alpha)\)
Recall that,
$$ \begin{align} &\textsf{Pos}_{0}(\alpha) = \textsf{Pos}(\alpha)\cup\{0\} \\ &\textsf{Follow}(\alpha, i) = \{j \mid (i, j) \in \textsf{Follow}(\alpha)\} \\ &\textsf{Follow}(\alpha) = \{(i, j) \mid u\sigma_{i}\sigma_{j}v \in \mathcal{L}(\overline{\alpha})\} \end{align} $$
Then we have,
$$ \textsf{F}(\alpha) = \{(\textsf{Follow}(\alpha, i), \varepsilon(i)) \mid i \in \textsf{Pos}_{0}(\alpha)\} $$
We've seen all of the parts of this before, but I want to spend a bit of time drawing out an important consequence of this definition. For a set \(A\), the number of elements in the set (its cardinality) is denoted \(|A|\). Now \(\textsf{F}(\alpha)\) has at most one member for each element in \(\textsf{Pos}_{0}(\alpha)\), therefore \(|\textsf{F}(\alpha)| \leq |\textsf{Pos}_{0}(\alpha)|\). So using this construction, \(\mathcal{A}_{\text{F}}\) is guaranteed to never exceed the number of states in \(\mathcal{A}_{\text{POS}}\).
Continuing our example, \(\overline{\alpha} = (a_{1}{*}|b_{2})a_{3}\),
$$ \begin{align} \textsf{First}(\alpha) &= \{1, 2, 3\} \\ \textsf{Follow}(\alpha) &= \{(1, 1), (1, 3), (2, 3)\} \\[10pt] (\textsf{Follow}(\alpha, 0), \varepsilon(0)) &= (\{1, 2, 3\}, \emptyset) \\ (\textsf{Follow}(\alpha, 1), \varepsilon(1)) &= (\{1, 3\}, \emptyset) \\ (\textsf{Follow}(\alpha, 2), \varepsilon(2)) &= (\{3\}, \emptyset) \\ (\textsf{Follow}(\alpha, 3), \varepsilon(3)) &= (\{\}, \varepsilon) \end{align} $$
So,
$$ \textsf{F}(\alpha) = \{(\{1, 2, 3\}, \emptyset), (\{1, 3\}, \emptyset), (\{3\}, \emptyset), (\{\}, \varepsilon)\} $$
Final States \(F_{\text{F}}\)
$$ F_{\text{F}} = \{(S, c) \in \textsf{F}(\alpha) \mid c = \varepsilon\} $$
We've again seen all the parts of this definition before now, though the notation is not entirely what we're used to. It's still straightforward to parse, reading: \((S, c)\) in \(\textsf{F}(\alpha)\) such that \(c = \varepsilon\).
With our example, \(\overline{\alpha} = (a_{1}{*}|b_{2})a_{3}\), there is only one state where \(c = \varepsilon\) and hence,
$$ F_{\text{F}} = \{(\{\}, \varepsilon)\} $$
Transition \(\delta_{\text{F}}\)
$$ \delta_{\text{F}}((S, c), \sigma) = \{(\textsf{Follow}(\alpha, j), \varepsilon(j)) \mid j \in \textsf{Select}(S, \sigma)\} $$
Here's finally something new, though we've actually seen \(\textsf{Select}\) before without realising it. Looking at the definition,
$$ \textsf{Select}(S, \sigma) = \{i \mid i \in S \text{ and } \overline{\sigma_{i}} = \sigma\} $$
this should hopefully look a little familiar to you. Let's go back to the definition of \(\delta_{POS}\),
$$ \delta_{POS}(i,\sigma) = \{j \mid j \in \textsf{Follow}(\alpha, i) \text{ and } \overline{\sigma_{j}} = \sigma\} $$
If we substitute \(S\) in \(\textsf{Select}\) with \(\textsf{Follow}(\alpha, i)\) then the definition for \(\delta_{POS}\) immediately pops out! Indeed, we can restate \(\delta_{POS}\) as,
$$ \delta_{POS}(i,\sigma) = \textsf{Select}(\textsf{Follow}(\alpha, i), \sigma) $$
\(\delta_{\text{F}}\) reverses the applications, first we \(\textsf{Select}\), then \(\textsf{Follow}\). Supposing, \(\overline{\alpha} = (a_{1}{*}|b_{2})a_{3}\), \((S, c) = (\{1, 3\}, \emptyset)\) and \(\sigma = a\),
$$ \begin{align} \textsf{Select}(\{1, 3\}, a) &= \{1, 3\} \\[10pt] \delta_{\text{F}}((\{1, 3\}, \emptyset), a) &= \{(\textsf{Follow}(\alpha, 1), \varepsilon(1)), (\textsf{Follow}(\alpha, 3), \varepsilon(3))\} \\ \delta_{\text{F}}((\{1, 3\}, \emptyset), a) &= \{(\{1, 3\}, \emptyset), (\{\}, \varepsilon)\} \end{align} $$
Implementation
We've already done the hard work of setting up the AST, parser, and automata structure, which makes this implementation both significantly easier and quicker than the one for \(\mathcal{A}_{\text{POS}}\). This is a good example of the compounding effect of prior work shortening the path for future work.
Generic States
To accommodate the Follow automata we only need to make one change to our Automata base class, which is to make the type of the state generic. This is simple to do, although since we're not using Python 3.12 we don't get the benefit of the lovely new type parameter syntax.
# automata/impl.py
from abc import ABC, abstractmethod
from automata.tree import Node
from typing import Generic, Self, TypeVar
# generic state type variable
T = TypeVar("T")
class Automata(ABC, Generic[T]):
@classmethod
@abstractmethod
def from_node(cls, node: Node) -> Self:
raise NotImplementedError
@property
@abstractmethod
def final(self) -> set[T]:
raise NotImplementedError
@property
@abstractmethod
def initial(self) -> set[T]:
raise NotImplementedError
@abstractmethod
def transition(self, state: T, symbol: str) -> set[T]:
raise NotImplementedError
def accepts(self, word: str) -> bool:
states = self.initial
for symbol in word:
if len(states) == 0:
return False
states = {t for s in states for t in self.transition(s, symbol)}
return len(states.intersection(self.final)) > 0
\(\mathcal{A}_{\text{F}}\)
Here is the implementation, short and sweet. There's not much to note, other than the extra processing which we do in __init__ and the transition method. This extra processing could easily be optimised, or removed entirely, so much so that the construction of \(\mathcal{A}_{\text{F}}\) is not much more onerous than \(\mathcal{A}_{\text{POS}}\).
# automata/impl.py
from typing import TypeAlias
# a type alias helps keep function signatures clean, clear and under control
FollowState: TypeAlias = tuple[frozenset[int], bool]
class FollowAutomata(Automata):
def __init__(self, node: Node) -> None:
self.pos = node.pos()
self.first = node.first()
self.last_0 = node.last_0()
self.follow = node.follow()
# using frozen set because it's hashable
self.init = (frozenset(self.first), 0 in self.last_0)
self.states = {0: self.init}
for idx in node.pos():
f_set = frozenset({j for i, j in self.follow if i == idx})
self.states[idx] = (f_set, idx in self.last_0)
self.final_set = {(s, fin) for s, fin in self.states.values() if fin}
@classmethod
def from_node(cls, node: Node) -> Self:
return cls(node)
@property
def final(self) -> set[FollowState]:
return self.final_set
@property
def initial(self) -> set[FollowState]:
return {self.init}
def transition(self, state: FollowState, symbol: str) -> set[FollowState]:
select = {i for i in state[0] if self.pos[i] == symbol}
return {self.states[j] for j in select}
Testing
Now we can reap the rewards of our testing setup, parameterized by the list of engines. Simply add FollowAutomata to the engine list, and all our automata tests now run against it as well. Yay!
# tests/test_automata.py
ENGINES = [PositionAutomata, FollowAutomata]
State Diagrams
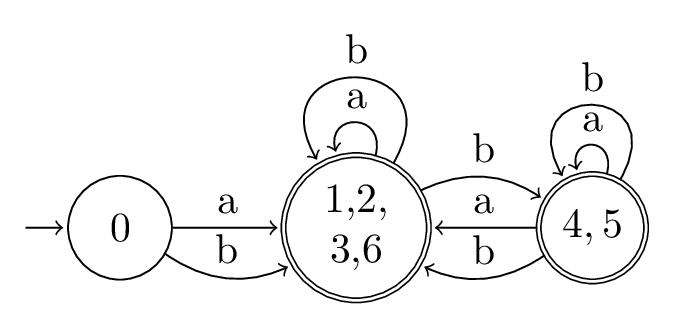
I want to quickly cover reading the style of state diagrams for Follow automata shown above. The implementation can help us with this, which is why I've left it till now. We'll reuse the example from the start of this post, \(\alpha = (a|b)(a{*}|ba{*}|b*)* \).
>>> from automata.impl import FollowAutomata
>>> from automata.parser import Parser
>>>
>>> node = Parser("(a|b)(a*|ba*|b*)*").parse()
>>> follow = FollowAutomata(node)
>>> for pos_i, state in follow.states.items():
... pos_i, state
...
... (0, (frozenset({1, 2}), False))
... (1, (frozenset({3, 4, 6}), True))
... (2, (frozenset({3, 4, 6}), True))
... (3, (frozenset({3, 4, 6}), True))
... (4, (frozenset({3, 4, 5, 6}), True))
... (5, (frozenset({3, 4, 5, 6}), True))
... (6, (frozenset({3, 4, 6}), True))
Remember that the boolean represents whether the state is final or not. There are three distinct states here, each indexed by one pos_i element. If we group them together we get something like:
>>> states = {
... (frozenset({1, 2}), False): [0],
... (frozenset({3, 4, 6}), True): [1, 2, 3, 6],
... (frozenset({3, 4, 5, 6}), True): [4, 5],
... }
>>> node.pos()
... {1: 'a', 2: 'b', 3: 'a', 4: 'b', 5: 'a', 6: 'b'}
which should give you all the info you need to figure out the state diagram,
Done
That's it, we've covered everything I wanted to cover here. There's just one more post left in this series that I really want to write: explaining the Mark Before automaton. This will bring us finally to Deterministic Finite Automata (DFA) after all this time spent with NFAs.
Mark Before constructions can give us the huge benefit of DFAs, \(\textsf{O}(n)\) time complexity to match a string, while reducing the impact of exploding numbers of states when constructing DFAs (up to \(2^{N}\) for a DFA constructed from an NFA with \(N\) states).
See you in the next one!
Postscript: Epsilon-Omissions
The classic go to resource for learning about implementing regex with automata is the article Regular Expression Matching Can Be Simple And Fast by Russ Cox. This piece covers implementing Thompson's NFA regex construction in C.
This is where I myself first learnt about the practicalities of implementing regex with automata and it remains a good read and useful resource, so why have I not mentioned it before now, or covered Thompson's construction?
Well one big reason is that readers are already well served by the article, but my reason is that we can do better than only use NFAs with \(\varepsilon\)-transitions (aka \(\varepsilon\)-moves). Constructions like Position and Follow came about partially in response to the desire to construct NFAs without \(\varepsilon\)-transitions, and as they can be constructed directly they have an inherent advantage over using NFAs which are built via \(\varepsilon\)-elimination.
Using Thompson's construction (or other \(\varepsilon\)-NFAs) without considering more recent developments (remember that Follow is from 2003) means potentially leaving significant benefits on the table. Hopefully this series has made the way of the non-epsilon more accessible.
References
- Allauzen, C. and Mohri, M., 2006, August. A unified construction of the Glushkov, Follow, and Antimirov automata. In International Symposium on Mathematical Foundations of Computer Science (pp. 110-121). Berlin, Heidelberg: Springer Berlin Heidelberg. link
- Broda, S., Holzer, M., Maia, E., Moreira, N. and Reis, R., 2017, July. On the mother of all automata: the position automaton. In International Conference on Developments in Language Theory (pp. 134-146). Cham: Springer International Publishing. link
- Ilie, L. and Yu, S., 2003. Follow automata. Information and computation, 186(1), pp.140-162. link