This is the first post in a series on coding up algorithms for constructing automata from regexes.
A quick note before we begin: I will link to relevant wikipedia pages, but in my opinion these pages are often not very comprehensible, so please do ignore them if you want and I hope I can give a more simplified and digestible intro to ideas you may be unfamiliar with.
Audience Assumptions: experience with regexes and basic knowledge of finite state machines. Code examples will be in no-frills python.
Intro
I've long been drawn to Finite State Machines (FSM) and Automata Theory. These areas of study enjoy a close relationship with the day to day practicalities of programs because, for all their theoretical nature, they directly specify methods for how we can make regexes usable. But drawing out that relationship is easier said than done! I've stared blankly at many a dense paper, willing myself to understand and achieving precisely nothing.
Anyway, I recently read Andrew Gallant's (AKA burntsushi) excellent and long (very long) post on the internals of the regex-automata crate. Naturally automata are discussed in detail, a central topic being Nondeterministic Finite Automata (NFA). One thing that jumped out to me was the section on future work mentioning Glushkov's NFA construction [2]. I was interested to learn about this, and more so, to investigate the various ways of constructing automata from regexes.
As you may have guessed from this intro, this was not as easy as looking up a few definitions and throwing together some code. It's more: Act 1 Scene 1, Marcus hits a brick wall of understanding. Eventually though I think I've found some clarity on these ideas, and this is what I want to share with you because it's what I wish I'd been able to read when I didn't understand. First off, you may be wondering why this post's title includes Position automata (PA) when I've yet to mention the term? Position automaton is just another name for Glushkov's automaton! Already one bit of clarity provided I hope, btw I'm just going to use the PA abbreviation from now on.
Defining Automata
In this series we'll be following the constructions provided in the paper: 'On the mother of all automata: the position automaton' [1] by Sabine Broda, Markus Holzer, Eva Maia, Nelma Moreira, and Rogério Reis. This paper is both clear and interesting, if you're curious how different automata relate to one another, or about the formal properties of various constructions, then it wont waste your time.
So what is an automata? Let's start with the formal definition and a simple code implementation. An automata \(A\) is a five-tuple:
$$A = \langle Q, \Sigma, \delta, I, F \rangle$$
- \(Q\) is a set of states that the automata can be in.
- \(\Sigma\) (capital sigma) is the set of symbols (or alphabet) this automata recognises. So for the string matching regexes we're used to, that is all the characters you can have in a string.
- \(\delta\) (small delta) is the transition function, which tells you how to go from a state and symbol to another state (or set of states).
- \(I\) is the "initial" or "start" state that the automata always starts in.
- \(F\) is the set of "final", "finishing" or "accepting" states. If a sequence of symbols puts the automata in a final state then the automata "accepts" the sequence. The initial state can be final (a member of \(F\)).
Let's implement this in a very literal fashion, to make the connections clear. Supposing states are just integers, and symbols are characters in a string.
class Automata:
def __init__(self):
self.states: set[int] # Q
self.symbols: set[str] # Sigma
self.initial: int # I
self.final: set[int] # F
# delta
@staticmethod
def transition(state: int, symbol: str) -> int | None:
# return None when the given (state, symbol) pair
# does not have a corresponding transition state
...
Simple enough, all we need to provide in order to have an automata are these five elements, and there are many possible ways of structuring this in code. Depending on how we fill out these parameters and define the transition function we'll end up with different kinds of automata. This is an important point I really want to stress, different automata constructions are just different ways of constructing the elements of the five-tuple.
State Diagrams
State diagrams are an intuitive visual aid to understanding automata. We depict all the states, indicating whether they are initial or final, and the transitions between them. Final states will always have a double ring.
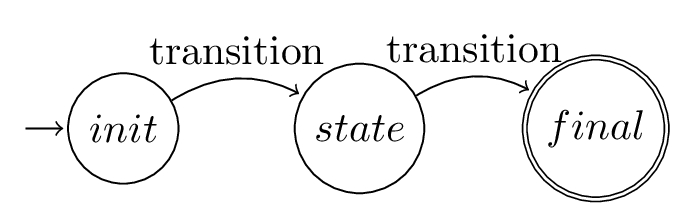
Example Automata
Consider the regex "ace", which can be converted to:
class Automata:
def __init__(self):
self.states: set[int] = {0, 1, 2, 3}
self.symbols: set[str] = set("abcdef")
self.initial: int = 0
self.final: set[int] = {3}
@staticmethod
def transition(state: int, symbol: str) -> int | None:
table = {
(0, "a"): 1,
(1, "c"): 2,
(2, "e"): 3,
}
return table.get((state, symbol))
This automata is depicted by this state diagram:
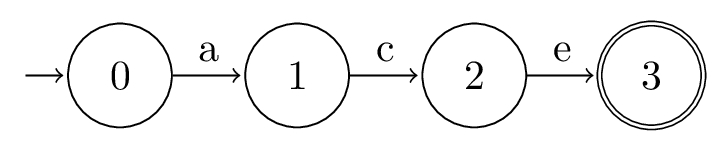
Position Automata
Okay, let's get stuck in to the details of PA, starting again with the formal definition:
$$\mathcal{A}_{\text{POS}}(\alpha) = \langle \textsf{Pos}_{0}(\alpha), \Sigma, \delta_{\text{POS}}, 0, \textsf{Last}_{0}(\alpha) \rangle$$
There's a lot more going on here, but we're just going to break it down element by element. To start with, \(\Sigma\) means exactly the same thing it did before, it's the set of symbols the automata recognises, and the start state is just whichever state corresponds to an index \(0\) (which will make more sense in a bit).
Set of States \(\textsf{Pos}_{0}(\alpha)\)
\(\textsf{Pos}_{0}(\alpha)\) is a set, and whats interesting is how we construct it. \(\alpha\) (alpha) is an element in the set of regular expressions... so \(\alpha\) is just a regex. Some examples:
- \(\alpha = \)
ab - \(\alpha = \)
ab+ - \(\alpha = \)
a*b
Warning: be careful when reading regexes containing alternation in papers. Alternation in code is often represented bya|b, but in papers you will see \(a+b\) used. Be careful not to confuse the 'plus' used in papers with the 'one or more' operator in code. Throughout this post I will use|for alternation.
\(\textsf{Pos}_{0}(\alpha)\) is the union of \(\textsf{Pos}(\alpha)\) and \(\{0\}\). \(\{0\}\) is set notation for the set with a single element: zero.
Okay so what's \(\textsf{Pos}(\alpha)\)? This set contains numbers used to index each symbol that occurs in a given regex. Let's say we have a regex:
$$\alpha = a(ba{*}b)*$$
Then the corresponding marked regular expression is given by indexing all the symbols, meaning we mark the elements of \(\Sigma\) which occur in the regex. It's important to note that we start counting indexes from \(1\) not \(0\).
$$\overline{\alpha} = a_{1}(b_{2}a_{3}{*}b_{4})*$$
Since \(\textsf{Pos}(\alpha)\) just contains these index numbers, we have:
$$\textsf{Pos}(\alpha) = \{1, 2, 3, 4\}$$
Finally we have:
$$\textsf{Pos}_{0}(\alpha) = \{0, 1, 2, 3, 4\}$$
Final States \(\textsf{Last}_{0}(\alpha)\)
Let's begin by talking about just \(\textsf{Last}(\alpha)\). Constructing this set is somewhat more involved, we'll have to cover several more definitions. Intuitively \(\textsf{Last}(\alpha)\) contains all the indexes of the symbols in \(\overline{\alpha}\) that can occur last in words matched by the regex. So when \(\alpha = \) ab, the position index for b would be in \(\textsf{Last}(\alpha)\).
This does come across in the formal definition, look for where \(\sigma_{i}\) is placed:
$$\textsf{Last}(\alpha) = \{i \mid w\sigma_{i}\in \mathcal{L}(\overline{\alpha})\}$$
This kind of set building notation is analogous to comprehensions in Python, we can read the above statement as: \(i\) for \(w\sigma_{i}\) in \(\mathcal{L}(\overline{\alpha})\). By the way, \(\sigma\in\Sigma\).
Set Comprehension Examples
\(A = \{e \mid e\in Elems\}\)
A = {e for e in Elems}
\(B = \{j \mid (i,j)\in Items \text{ and } i = 1\}\)
B = {j for (i, j) in Items if i == 1}
Now let's break down the parts of this definition starting with \(\mathcal{L}(\overline{\alpha})\). We've already covered that \(\overline{\alpha}\) is \(\alpha\) with symbols indexed, so let's simplify and ask what \(\mathcal{L}(\alpha)\) is.
\(\mathcal{L}(\alpha)\) is the language associated to \(\alpha\), or what this regex matches. The kind of thing a regex matches are words, \(w\). \(w\) is a member of \(\Sigma^{\star}\) which is the set of all combinations of symbols in \(\Sigma\).
- \(\Sigma = \{a, b, c, ...\}\)
- \(\Sigma^{\star} = \{a, aa, ..., ab, abb, ...\}\)
- \(w\in\Sigma^{\star}\)
- \(\mathcal{L}(\alpha)\subseteq\Sigma^{\star}\) (\(\mathcal{L}(\alpha)\) is a subset of \(\Sigma^{\star}\) as not all possible words may be accepted by \(\alpha\))
With \(\overline{\alpha}\) we have the language drawn from symbols with indexes given by \(\textsf{Pos}(\alpha)\). \(\mathcal{L}(\alpha)\) is often defined recursively, check the details below if you're interested.
\(\mathcal{L}(\alpha)\) Defined Recursively
- If \(\alpha = \varepsilon\), then \(\mathcal{L}(\alpha) = \{\varepsilon\}\) (\(\varepsilon\) is the empty word or string).
- If \(\alpha = a\), then \(\mathcal{L}(\alpha) = \{a\}\) where \(a\in\Sigma\).
- If \(\alpha = \beta\mid\gamma\), then \(\mathcal{L}(\alpha) = \mathcal{L}(\beta)\cup\mathcal{L}(\gamma)\) (alternation).
- If \(\alpha = \beta\gamma\), then \(\mathcal{L}(\alpha) = \mathcal{L}(\beta)\mathcal{L}(\gamma)\) where \(\mathcal{L}(\beta)\mathcal{L}(\gamma)\) is the set of all words where words from \(\mathcal{L}(\beta)\) are joined with words from \(\mathcal{L}(\gamma)\) (concatenation). Concatenation is sometimes also writen as \(\alpha = \beta\cdot\gamma\)
- If \(\alpha = \beta*\), then \(\mathcal{L}(\alpha)\) contains zero or more words from \(\mathcal{L}(\beta)\).
Using the same marked regex from earlier, \(\overline{\alpha} = a_{1}(b_{2}a_{3}{*}b_{4})*\), let's write down some of the words in its language (words that are matched by the regex).
$$\mathcal{L}(\overline{\alpha}) = \{a_{1}, a_{1}b_{2}b_{4}, a_{1}b_{2}a_{3}a_{3}b_{4}, ...\}$$
Looking at \(w\sigma_{i}\in \mathcal{L}(\overline{\alpha})\) from the definition of \(\textsf{Last}\), what are \(w\) and \(\sigma_{i}\) here? \(\sigma_{i}\) refers to the last indexed symbol of some word in \(\mathcal{L}(\overline{\alpha})\). So if \(w = a_{1}b_{2}b_{4}\), then \(\sigma_{i} = b_{4}\) and \(i = 4\) (this abuses the notation of \(w\) a bit).
Hopefully it's relatively clear that our example regex will only ever have \(a_{1}\) and \(b_{4}\) in the last position, hence:
$$\textsf{Last}(\alpha) = \{1, 4\}$$
We're not done I'm afraid! 😵💫
What we actually wanted was \(\textsf{Last}_{0}(\alpha)\), which extends \(\textsf{Last}\) to possibly include the starting index \(0\). Intuitively, what we want to know is if the regex \(\alpha\) accepts the empty word (or string), usually written as \(\varepsilon\) (epsilon).
Starting as always with the definition:
$$\textsf{Last}_{0}(\alpha) = \textsf{Last}(\alpha) \cup \varepsilon(\alpha)\{0\}$$
We know what \(\textsf{Last}(\alpha)\) is, so we just need to know what this other set \(\varepsilon(\alpha)\{0\}\) is (it must be a set because we perform a union).
This particular bit of notation is somewhat peculiar, not least because \(\varepsilon\) is used as a function, but it's just a very concise way of choosing and applying functions using notational abuse (admitted to by the authors). Broda et al. define \(\varepsilon(\alpha)\) as:
$$\varepsilon(\alpha) = \begin{cases}\varepsilon \text{ if }\varepsilon \in \mathcal{L}(\alpha)\\ \emptyset \text{ otherwise}\end{cases}$$
Python Sketch
import re
def get_language(alpha: re.Pattern) -> set[str]:
...
def nullable(alpha: re.Pattern) -> str | set[str]:
if "" in get_language(alpha):
return ""
return set()
\(\emptyset\) is the empty set. This function just says that \(\varepsilon(\alpha)\) returns the empty word if this is in the language for \(\alpha\), otherwise it returns the empty set. We also have:
$$\varepsilon S = S$$ $$\emptyset S = \emptyset$$
Where \(S\) is any set. So \(\varepsilon\) applied to any set is just that set, and applying \(\emptyset\) returns the empty set.
Back to our example \(\overline{\alpha} = a_{1}(b_{2}a_{3}{*}b_{4})*\). This regex cannot accept the empty word, so:
$$ \begin{align} \varepsilon(\alpha) &= \emptyset \\ \varepsilon(\alpha)\{0\} &= \emptyset\{0\} \\ \emptyset\{0\} &= \emptyset \end{align} $$
And after all that! \(\textsf{Last}_{0}(\alpha) = \textsf{Last}(\alpha) \cup \emptyset\), thus:
$$\textsf{Last}_{0}(\alpha) = \{1, 4\}$$
😵
Transition \(\delta_{POS}\)
Last one, and it's a biggie: the transition function \(\delta_{POS}\). Of course, the definition:
$$\delta_{POS}(i,\sigma) = \{j \mid j \in \textsf{Follow}(\alpha, i) \text{ and } \sigma = \overline{\sigma_{j}}\}$$
Python Sketch
import re
regex: re.Pattern = ...
POS_0 = ... # symbols with indexes
def follow(alpha: re.Pattern, index: int) -> set[int]:
...
def delta_pos(index: int, symbol: str) -> set[int]:
return {j for j in follow(regex, index) if symbol == POS_0[j]}
Nothing too fancy, and understanding this is just down to grasping \(\textsf{Follow}\) in all it's forms. As before we're going to explore the parts until we bottom out on definitions.
$$\textsf{Follow}(\alpha, i) = \{j \mid (i, j) \in \textsf{Follow}(\alpha)\}$$
We still don't know what \(\textsf{Follow}(\alpha)\) is, so lets keep going.
$$\textsf{Follow}(\alpha) = \{(i, j) \mid u\sigma_{i}\sigma_{j}v \in \mathcal{L}(\overline{\alpha})\}$$
Aha! This looks familiar, and hopefully this form helps guide the intuition that "following" is just about finding what symbols can follow other symbols in the language of our regex. Essentially \(\textsf{Follow}\) determines pairs of marked symbol indexes where the \(j\)'th symbol follows the \(i\)'th symbol.
Returning to our example \(\overline{\alpha} = a_{1}(b_{2}a_{3}{*}b_{4})*\) and some of it's matching words:
$$\mathcal{L}(\overline{\alpha}) = \{a_{1}, a_{1}b_{2}b_{4}, a_{1}b_{2}a_{3}a_{3}b_{4}, ...\}$$
Let's consider \(u\sigma_{i}\sigma_{j}v \in \mathcal{L}(\overline{\alpha})\). Well \(u\sigma_{i}\sigma_{j}v\) is really just some \(w\) and the two sigmas are just symbols in \(\Sigma\) that are consecutive in \(w\). So if \(w = a_{1}b_{2}a_{3}a_{3}b_{4}\), then (choosing one pair) \(\sigma_{i} = b_{2}\), \(\sigma_{j} = a_{3}\), and \((i, j) = (2, 3)\). The set in full:
$$\textsf{Follow}(\alpha) = \{(1, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 2)\}$$
Which makes \(\textsf{Follow}(\alpha, i)\) easy to understand, supposing \(i = 2\):
$$\textsf{Follow}(\alpha, 2) = \{3, 4\}$$
That's almost everything for \(\textsf{Follow}\), but one problem remains: how do we follow from \(0\)? This is handled simply enough:
$$\textsf{Follow}(\alpha, 0) = \textsf{First}(\alpha)$$
At which point you may be exclaiming "not another definition" in frustration! Don't worry, \(\textsf{First}\) is very straightforward for us now, it's definition is almost identical to \(\textsf{Last}\), except in the obvious way.
$$\textsf{First}(\alpha) = \{i \mid \sigma_{i}w\in \mathcal{L}(\overline{\alpha})\}$$
Yep, we just put \(\sigma_{i}\) before \(w\). I'm not going to go through all the explanatory steps again (exercise for the reader as they say), suffice to state that for our example regex, we have:
$$\textsf{First}(\alpha) = \{1\}$$
Back to the transition function, let's put in some values and see what we get.
$$ \begin{align} \delta_{POS}(i,\sigma) &= \{j \mid j \in \textsf{Follow}(\alpha, i) \text{ and } \sigma = \overline{\sigma_{j}}\} \\ \delta_{POS}(2, a) &= \{j \mid j \in \{3, 4\} \text{ and } a = \overline{\sigma_{j}}\} \\ \delta_{POS}(2, a) &= \{3\} \end{align} $$
Because \(\overline{\sigma_{3}} = a\) and \(\overline{\sigma_{4}} = b\).
Putting it All Together
$$\mathcal{A}_{\text{POS}}(\alpha) = \langle \textsf{Pos}_{0}(\alpha), \Sigma, \delta_{\text{POS}}, 0, \textsf{Last}_{0}(\alpha) \rangle$$
Let \(\alpha = a(ba{*}b)*\), and so we have \(\overline{\alpha} = a_{1}(b_{2}a_{3}{*}b_{4})*\).
- \(\Sigma = abcd...\)
- \(\textsf{Pos}_{0}(\alpha) = \{0, 1, 2, 3, 4\}\)
- \(\textsf{Follow}(\alpha) = \{(1, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 2)\}\)
- \(\textsf{Follow}(\alpha, 0) = \{1\}\)
- \(\textsf{Last}_{0}(\alpha) = \{1, 4\}\)
The position automaton for \(\alpha\) is depicted as:
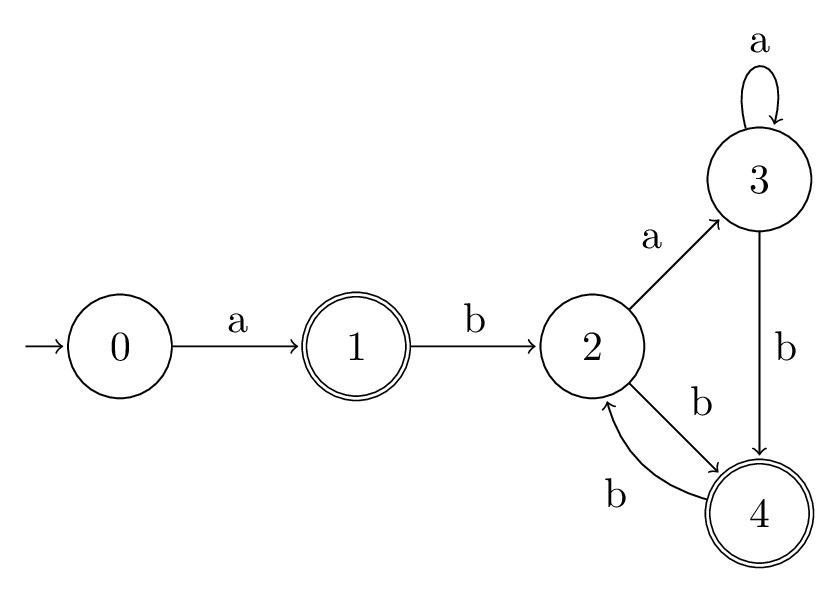
Example \((a| b{*})a\)
Let \(\alpha = (a|b{*})a\), so \(\overline{\alpha} = (a_{1} | b_{2}{*})a_{3}\).
- \(\textsf{Pos}_{0}(\alpha) = \{0, 1, 2, 3\}\)
- \(\textsf{Follow}(\alpha) = \{(1, 3), (2, 2), (2, 3)\}\)
- \(\textsf{Follow}(\alpha, 0) = \{1, 2, 3\}\)
- \(\textsf{Last}_{0}(\alpha) = \{3\}\)
State diagram:
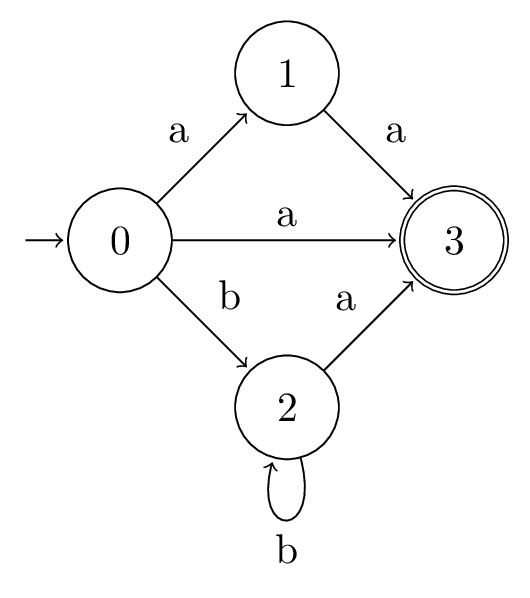
This diagram let's us observe clearly why PA is a non-deterministic finite automata, because multiple states can be returned from the transition function, instead of only ever returning one. For example, if \(i = 0\) and \(\sigma = a\), then:
$$\delta_{POS}(0, a) = \{1, 3\}$$Example \(a{*}b*\)
Let \(\alpha = a{*}b*\), so \(\overline{\alpha} = a_{1}{*}b_{2}*\).
- \(\textsf{Pos}_{0}(\alpha) = \{0, 1, 2\}\)
- \(\textsf{Follow}(\alpha) = \{(1, 1), (1, 2), (2, 2)\}\)
- \(\textsf{Follow}(\alpha, 0) = \{1, 2\}\)
- \(\textsf{Last}_{0}(\alpha) = \{0, 1, 2\}\)
State diagram:
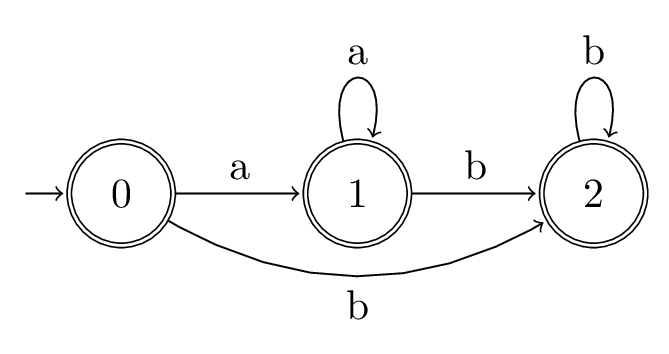
In this example we can see that, since this regex accepts the empty word \(\varepsilon\), the initial state \(0\) is also a final state.
Where To Now?
We made it! Although I don't think all the details we've been through necessarily lend themselves to a natural and intuitive mental model of PA, what they do provide is a clear mechanics of how we can construct these automata. Since using these definitions will firm up our understanding of these ideas, and since we currently we have no proper implementation, our path forward is easy to choose. In the next post of this series we'll work on a more serious Python implementation of the construction of PA from regexes using the definitions we've presented here.
Something of interest, the notions of \(\textsf{First}\), \(\textsf{Last}\) and \(\textsf{Follow}\) that we have encountered here pop up in a lot of places, indeed this whole idea of labelling positions and tracking relationships between them is very useful. For example, the Rust project uses these sets to help handle ambiguity in declarative macros (AKA macro-by-example).
Acknowledgements
Thanks to my friend Declan Kolakowski for proof reading the draft of this post.
References
- Broda, S., Holzer, M., Maia, E., Moreira, N. and Reis, R., 2017, July. On the mother of all automata: the position automaton. In International Conference on Developments in Language Theory (pp. 134-146). Cham: Springer International Publishing. link
- Glushkov, V.M., 1961. The abstract theory of automata. Russian Mathematical Surveys, 16(5), p.1.